Weiterbildung – Online lernen – Kaufmännisches Rechnen – Verteilungsrechnung, Anteile berechnen, Anleitung, Formel & 3 Übungen kostenlos
In diesem Beitrag lernen Sie, wie Sie Anteile korrekt berechnen und eine Verteilungsrechnung mit einem Verteilungsschlüssel durchführen. Schritt für Schritt erfahren Sie, wie Sie einen Verteilungsschlüssel erstellen, Anteile zuordnen und die passende Formel anwenden.
Zur Vertiefung erhalten Sie eine verständliche Anleitung, ein anschauliches Beispiel sowie Übungen und Aufgaben zum Üben – ideal für Schule, Ausbildung oder berufliche Praxis.
Verteilungsrechnung einfach erklärt: So berechnen Sie Anteile korrekt
Die Verteilungsrechnung (auch: Anteile berechnen, proportionale Verteilung) hilft Ihnen dabei, eine Gesamtsumme fair und nachvollziehbar auf mehrere Bereiche aufzuteilen. Grundlage ist ein Verteilungsschlüssel. Dieser Schlüssel besteht aus Zahlen, die das Verhältnis der Aufteilung beschreiben (z. B. 3 : 2 : 4 : 3).
Das Prinzip ist immer gleich: Sie bilden zuerst die Summe aller Schlüsselwerte. Danach teilen Sie den Gesamtwert durch diese Summe. So erhalten Sie den Wert von 1 Anteil (Einheitswert). Anschließend multiplizieren Sie den Einheitswert mit den jeweiligen Schlüsselwerten – so entstehen die Teilbeträge pro Kategorie.
Wofür braucht man die Verteilungsrechnung in Schule und Praxis?
Die Verteilungsrechnung begegnet Ihnen häufiger, als viele denken – sowohl im kaufmännischen Bereich als auch in mathematischen Aufgaben. Typische Anwendungsfälle sind:
- Kostenverteilung auf Abteilungen (z. B. Verwaltung, Lager, Verkauf)
- Gewinnverteilung auf Gesellschafter nach Beteiligung (Kapitalanteile)
- Budgetverteilung auf Projekte oder Teams nach einem Schlüssel
- Ressourcenverteilung (Zeit, Material, Flächen) nach Gewichtung
- Mathematik-Aufgaben zur proportionalen Verteilung / Verhältnisrechnung
Wenn Sie zusätzlich die Grundlagen der Verhältnisrechnung auffrischen möchten, hilft oft der Dreisatz als Denkmuster. Dazu finden Sie bei Bildungsbibel bereits passende Inhalte (z. B. zur Multiplikation und zur Bruchrechnung).
Formel für die Verteilungsrechnung (Rechenschema)
Bei der Verteilungsrechnung handelt es sich weniger um eine einzelne Formel, sondern um ein klares Rechenschema. Am übersichtlichsten ist eine Tabelle – trotzdem können Sie die Kernregel als Formel notieren:
Formel: Anteil je Kategorie = (Gesamtwert / Summe der Verteilungsschlüssel) × Verteilungsschlüssel der Kategorie
Merken Sie sich zusätzlich diese drei Schritte – damit lösen Sie praktisch jede Aufgabe zur Verteilungsrechnung:
- Schlüssel sumieren (Summe der Anteile bilden)
- Einheitswert berechnen (Gesamtwert ÷ Schlüssel-Summe)
- Teilbeträge berechnen (Einheitswert × jeweiliger Schlüssel)
Beispiel für die Verteilungsrechnung (mit Tabelle)
Folgendes Beispiel zeigt, wie Sie bei der Verteilungsrechnung Schritt für Schritt vorgehen. Sie sehen dabei auch, wie hilfreich eine Tabelle ist – für Übersicht, Kontrolle und das Vermeiden typischer Rechenfehler.
Beispiel: Ein Unternehmen hat Kosten in Höhe von 120.000 € zu verbuchen. Davon entfallen 3 Anteile auf die Buchhaltung. 2 Anteile auf das Lager. 4 Anteile auf den Verkauf sowie 3 Anteile auf den Einkauf. Wie hoch sind die Kosten für jede Abteilung?
Schritt 1: Summe über die Anteile bilden
Schritt 1 – Sie bilden die Summe über die einzelnen Anteile und notieren diese spaltenförmig nach unten, den jeweiligen Abteilungen zugeordnet.

Die Summe des Verteilungsschlüssels = 3 + 2 + 4 + 3 = 12
Schritt 2: Einheitswert (Wert von 1 Anteil) berechnen
Schritt 2 – Die Kosten betragen 120.000 € und werden nun durch die Summe der Anteile geteilt. Somit erhalten Sie den Eurobetrag für 1 Anteil (Einheitswert).
Beispiel: 120.000 / 12 = 10.000,00 €
Der Anteil, welcher auf 1 Anteil entfällt, entspricht also 10.000 € an Kosten.

Schritt 3: Verteilungsschlüssel mit dem Einheitswert multiplizieren
Schritt 3 – Durch die Multiplikation mit dem Einheitswert und dem Verteilungsschlüssel jeder Abteilung erhalten Sie die Kosten pro Abteilung.
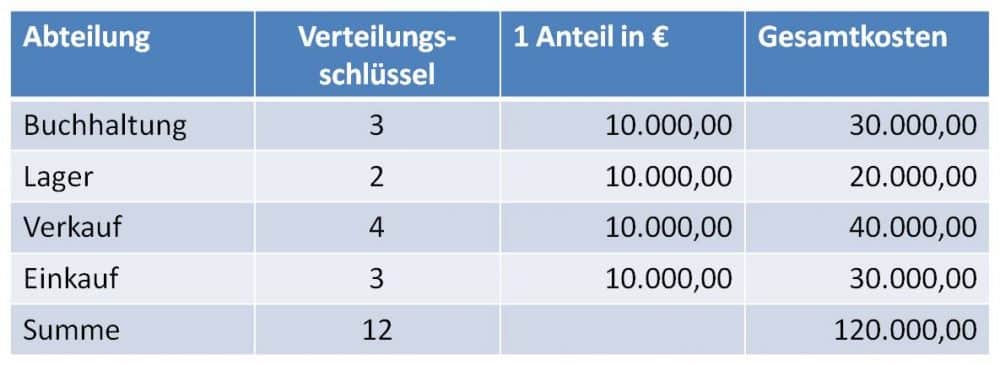
Somit sind die Gesamtkosten von 120.000,00 € auf die 4 Abteilungen mithilfe des Verteilungsschlüssels verteilt. Durch die Bildung der Summe über die Gesamtkosten je Abteilung können Sie prüfen, ob Sie die Kosten richtig verteilt haben.
| Abteilung | Schlüssel | Einheitswert | Rechnung | Teilbetrag |
|---|---|---|---|---|
| Buchhaltung | 3 | 10.000 € | 3 × 10.000 € | 30.000 € |
| Lager | 2 | 10.000 € | 2 × 10.000 € | 20.000 € |
| Verkauf | 4 | 10.000 € | 4 × 10.000 € | 40.000 € |
| Einkauf | 3 | 10.000 € | 3 × 10.000 € | 30.000 € |
| Summe | 12 | – | – | 120.000 € |
Schnelle Kontrolle: So prüfen Sie Ihr Ergebnis
- Summencheck: Addieren Sie alle Teilbeträge – das Ergebnis muss die Gesamtsumme ergeben.
- Verhältnischeck: Höherer Schlüsselwert = höherer Anteil (bei proportionaler Verteilung).
- Plausibilität: Passt die Verteilung zur Aufgabenstellung (z. B. größte Abteilung bekommt den höchsten Anteil)?
Verteilungsschlüssel bilden: So finden Sie das richtige Verhältnis
Nicht jeder Sachverhalt hat einen fertigen Verteilungsschlüssel. Häufig müssen Sie ihn zuerst aus den gegebenen Daten ableiten – zum Beispiel aus Flächen (m²), Mitarbeiterzahlen, Umsatzanteilen, Maschinenstunden oder Kapitalanteilen. Der Verteilungsschlüssel ist dann das vereinfache Verhältnis dieser Werte.
Wichtig: Der Schlüssel muss nicht „schön“ aussehen – er muss zur Aufgabenlogik passen. In vielen Fällen können Sie die Werte sinnvoll kürzen, damit die Rechnung übersichtlicher wird.
Beispiel: Verteilungsschlüssel aus Beteiligungen bilden
Beispiel: 3 Gesellschafter haben verschiedene Beteiligungen an einem Unternehmen. Gesellschafter A hat 150.000 € eingebracht, Gesellschafter B 300.000 € und Gesellschafter C 450.000 €.
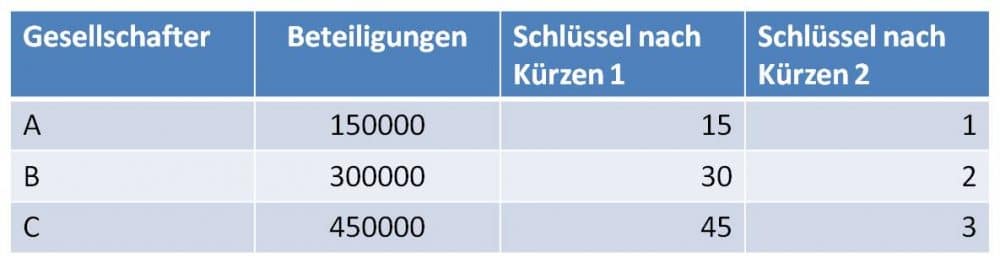
Wenn Sie die Beteiligungen in € so weit kürzen wie möglich, erhalten Sie einen Verteilungsschlüssel, der die Anwendung und weitere Berechnungen erleichtert. In obigem Beispiel wird zuerst durch 10.000 gekürzt. Daraus werden die Werte 15, 30 und 45. Diese Werte können Sie weiter kürzen – hier durch 15. Sie erhalten den Verteilungsschlüssel 1 : 2 : 3.
Zusatz-Beispiel: Gewinnverteilung mit Verteilungsrechnung
Angenommen, es sollen 60.000 € Gewinn nach dem Schlüssel 1 : 2 : 3 verteilt werden. Dann rechnen Sie genauso wie bei den Kosten:
- Summe Schlüssel: 1 + 2 + 3 = 6
- Einheitswert: 60.000 € ÷ 6 = 10.000 €
- Anteile: A = 1×10.000 € = 10.000 €, B = 2×10.000 € = 20.000 €, C = 3×10.000 € = 30.000 €
Damit sehen Sie: Die Verteilungsrechnung ist ein einheitliches Verfahren – egal, ob Sie Kosten, Gewinn oder Budget verteilen.
Verteilungsrechnung mit Brüchen: Anteile berechnen, wenn Bruchteile vorgegeben sind
Sollten die Angaben als Bruch vorliegen, müssen Sie die Brüche zunächst auf den gleichen Hauptnenner bringen und erweitern. Danach bilden die Zähler der Brüche den Verteilungsschlüssel. Mehr zur Addition in der Bruchrechnung lernen.
Beispiel: A erhält 1/4, B erhält 1/2 und C erhält 1/5 von einem bestimmten Kapital. Der Rest geht an D. Sie sollen den Schlüssel für die Verteilung berechnen.
Berechnung: Als erstes müssen Sie den Hauptnenner bilden, notfalls mit der Primfaktorzerlegung. Da die Nenner 2, 4 und 5 vorkommen, ist das kleinste gemeinsame Vielfache 20. Das ist der Hauptnenner. Jetzt erweitern Sie die Brüche auf 20 und ermitteln den Rest.
- A) 1/4 = 5/20
- B) 1/2 = 10/20
- C) 1/5 = 4/20
- D) Rest = 1/20
Der Verteilungsschlüssel mit Brüchen lautet in diesem Beispiel: 5 : 10 : 4 : 1.
Typische Fehler bei Brüchen (und wie Sie sie vermeiden)
- Hauptnenner falsch: Prüfen Sie das kgV der Nenner sorgfältig.
- Rest vergessen: Wenn „der Rest“ an eine Person/Gruppe geht, muss die Summe der Anteile wieder 1 (bzw. der Hauptnenner) ergeben.
- Zähler/Nenner vertauscht: Für den Schlüssel zählen die Zähler (nach Erweiterung), nicht die Nenner.
Verteilungsrechnung in der Kostenrechnung: Verteilungsschlüssel in der Praxis
In Unternehmen werden Gemeinkosten häufig mit einem Verteilungsschlüssel (auch: Umlageschlüssel) auf Kostenstellen verteilt. Die Idee ist ähnlich: Ein gemeinsamer Betrag (z. B. Miete, Energie, Verwaltung) wird nach einem nachvollziehbaren Maßstab verteilt, z. B. nach Fläche (m²), Mitarbeiterzahl, Umsatz oder Maschinenstunden.
Wenn Sie dazu Begriffe nachschlagen möchten, finden Sie gute Erklärungen außerhalb von Wikipedia zum Beispiel hier (externe Quellen, öffnen in neuem Tab): Gabler Wirtschaftslexikon: Kostenstelle.
Mini-Checkliste: Ein guter Verteilungsschlüssel erfüllt diese Kriterien
- Nachvollziehbar: Ein Außenstehender kann die Logik verstehen.
- Messbar: Die Basiswerte (z. B. m², Stunden, Köpfe) sind belegbar.
- Konsequent: Gleiche Fälle werden gleich behandelt.
- Plausibel: Der Schlüssel passt zum Kostenverursacherprinzip (wer verursacht, trägt).
Gerade bei kaufmännischen Aufgaben lohnt es sich, den Schlüssel kurz in Worten zu erklären (z. B. „Verteilung nach Fläche“). Das bringt viele Punkte – und reduziert Fehler.
Übungen, Aufgaben oder Arbeitsblätter für die Verteilungsrechnung kostenlos downloaden
Hier können Sie sich zusätzlich Übungen bzw. Aufgaben für die Verteilungsrechnung oder zum Anteile berechnen im PDF-Format kostenlos downloaden. Diese Arbeitsblätter sind zum Ausdrucken sowie zum Lernen geeignet.
Übung 1 (PDF)
Übung 2 (PDF)
Übung 3 (PDF)
Empfohlene Übungsroutine (15–30 Minuten pro Blatt)
- Lesen Sie die Aufgabe einmal komplett und markieren Sie: Gesamtsumme, Schlüssel, Kategorien.
- Erstellen Sie eine kleine Tabelle: Kategorie | Schlüssel | Rechnung | Ergebnis.
- Rechnen Sie den Einheitswert aus und tragen Sie ihn ein.
- Multiplizieren Sie und machen Sie danach den Summencheck (muss wieder die Gesamtsumme ergeben).
Video zur Verteilungsrechnung
FAQ: Häufige Fragen zur Verteilungsrechnung
Was ist der Einheitswert bei der Verteilungsrechnung?
Der Einheitswert ist der Wert von 1 Anteil. Sie berechnen ihn, indem Sie den Gesamtwert durch die Summe der Schlüsselwerte teilen. Danach multiplizieren Sie ihn mit den einzelnen Schlüsseln.
Wie erkenne ich, ob ich proportional verteilt habe?
Wenn der Schlüssel doppelt so groß ist, muss auch der Anteil (Teilbetrag) doppelt so groß sein – bei gleicher Ausgangssumme. Prüfen Sie das mit einem kurzen Verhältnischeck.
Was mache ich, wenn „der Rest“ verteilt werden soll?
Wenn Anteile als Brüche vorgegeben sind (z. B. 1/4, 1/2, 1/5), müssen Sie zuerst den Hauptnenner bilden, die Brüche erweitern und dann den Rest als Differenz zum Hauptnenner bestimmen.
Gibt es auch eine Verteilungsrechnung mit Prozenten?
Ja. Prozente sind ebenfalls Anteile. Wenn die Summe der Prozente 100 % ergibt, können Sie direkt rechnen: Anteil = Gesamtwert × Prozentsatz. Wenn die Prozente nicht 100 % ergeben (oder gemischte Angaben vorliegen), ist die Verteilungsrechnung über Einheitswert und Schlüssel oft sicherer.
Häufige Fehler (und wie Sie sie vermeiden)
- Schlüssel-Summe falsch: Addieren Sie die Schlüsselwerte sauber und prüfen Sie die Summe.
- Einheiten gemischt: Achten Sie auf € / Stück / Stunden. Der Einheitswert hat dieselbe Einheit wie die Gesamtsumme.
- Rundungsfehler: Bei Centbeträgen runden Sie erst am Ende (oder verteilen Rundungsdifferenzen nachvollziehbar).
- Brutto/Netto verwechselt: In kaufmännischen Aufgaben muss klar sein, welche Summe verteilt wird (z. B. Kosten netto).
Wenn Sie Ihre Grundlagen im kaufmännischen Rechnen weiter ausbauen möchten, sind diese externen Quellen (keine Wikipedia) häufig hilfreich: Gabler Wirtschaftslexikon (Begriffe nachschlagen) und für zusätzliche Aufgaben zur Gewinnverteilung dieses PDF: Übungen zur Gewinnverteilung.
Weitere Informationen
Diese Informationen könnten Sie ebenfalls interessieren:
- Die Excel Übungen zur Verteilungsrechnung finden.
- Den gewogenen Durchschnitt oder gewichteten Mittel berechnen lernen.
- Der geometrische Durchschnitt oder das geometrische Mittel berechnen lernen.

