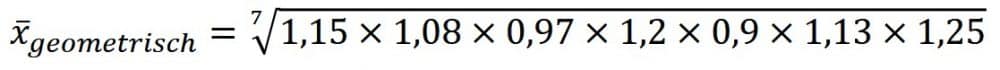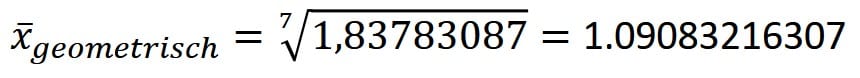Sie lernen in diesem Beitrag mehr zum Thema geometrisches Mittel bzw. zum geometrischen Durchschnitt berechnen. Hier lernen Sie anhand der Formel und einem Beispiel, wie Sie den geometrischen Durchschnitt berechnen können.
Zusätzlich erhalten Sie Aufgaben und Übungen sowie eine Anleitung zum üben sowie vertiefen der Inhalte.
Inhaltsverzeichnis
Geometrisches Mittel oder Durchschnitt – Was ist das?
Der geometrische Durchschnitt bzw. das geometrische Mittel wird berechnet in dem man das Produkt über bestimmte Werte ermittelt. Danach zieht man die Wurzel unter Berücksichtigung der Anzahl der einzelnen Werte. Diese Kennzahl wird meist benötigt, als Lageparameter, um in der deskriptiven Statistik Veränderungen feststellen zu können.
Formel um ein geometrisches Mittel zu berechnen
Wie oben schon genannt besteht die Formel zur Berechnung des geometrischen Mittels darin, dass man das Produkt der einzelnen Werte bildet. Danach zieht man die Wurzel unter Berücksichtigung der Anzahl der summierten Werte. In folgender Abbildung können Sie nachvollziehen was damit gemeint ist:
Beispiel und Anleitung zum geometrischen Mittel berechnen
Folgendes Beispiel zeigt auf, wie Sie den geometrischen Durchschnitt bzw. Mittelwert berechnen können.
Beispiel: Kauf von Aktien und deren Wertveränderungen Sie haben im Jahr 2010 Aktien eines Unternehmens gekauft. Seitdem hat die Aktie folgende Wertveränderungen erfahren:
- 2010: + 15 %
- 2011: + 8 %
- 2012: -3 %
- 2013: + 20 %
- 2014: – 10 %
- 2015: + 13 %
- 2016: + 25 %
Berechnen Sie das geometrische Mittel für diese Aktie, dass heißt, wie hoch ist die durchschnittliche Wertveränderung.
Faktoren festlegen
Schritt 1 – Um das geometrische Mittel zu berechnen ist es nötig die Rechenfaktoren der Wertsteigerung bzw. Wertminderung zu berücksichtigen. Danach in die Formel einzusetzen. Die Rechenfaktoren für die Jahre 2010 bis 2016 sind folgende:
- 2010: 1,15
- 2011: 1,08
- 2012: 0,97
- 2013: 1,20
- 2014: 0,90
- 2015: 1,13
- 2016: 1,25
Die Faktoren errechnen sich, wie bei der Zinseszinsrechnung aus dem Wert q = 1+(p/100). Exemplarisch für das erste Jahr = 1+(15/100) = 1,15.
Einsetzen der Werte in die Formel für das geometrische Mittel
Schritt 2 – Jetzt setzen Sie die Faktoren in die Formel für den geometrischen Durchschnitt ein. Wurzel n=7 (für die 7 Werte bzw. Jahre).
Geometrisches Mittel oder den geometrischen Durchschnitt bilden
Schritt 3 – Danach rechnen Sie das Produkt der 7 Werte aus und erhalten 1,83783087.
Daraus ziehen Sie die 7. Wurzel und erhalten nun 1.09083216307. Hier erkennt man die durchschnittliche Wertveränderung von + 9,08 %.
Antwort: Die Aktie hat eine jährliche Wertsteigerung von 9,08 % erreicht.
Übungen, Aufgaben oder Arbeitsblätter zum geometrischen Mittel oder Durchschnitt kostenlos downloaden
Hier können Sie sich zusätzlich Übungen für die Berechnung des geometrischen Mittels bzw. der geometrischen Durchschnittsrechnung im PDF-Format kostenlos downloaden. Diese Arbeitsblätter sind zum Ausdrucken sowie zum Lernen der Mittelwertberechnung geeignet.
Weitere Infos
Diese Infos könnten Sie ebenfalls interessieren:
- Den Mittelwert in Excel berechnen lernen.
- Den gewogenen Durchschnitt bzw. das gewogene arithmetische Mittel berechnen lernen.
- Weiterhin lernen Sie hier., wie Sie den einfachen Durchschnitt bzw. Mittelwert berechnen.
- Weitere Übungen zum geometrischen Mittel finden.