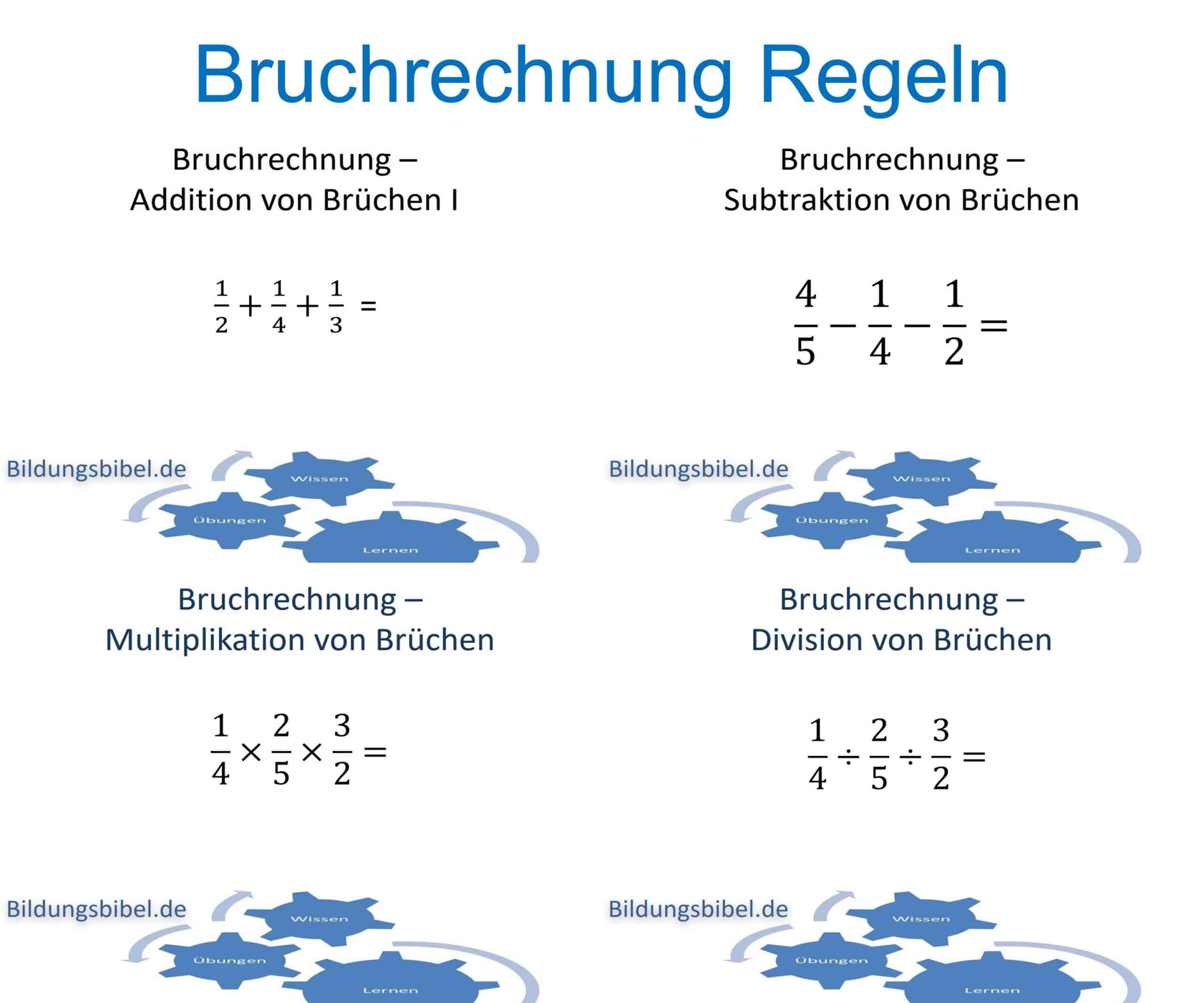
Weiterbildung – Online lernen – Kaufmännisches Rechnen – Bruchrechnung Regeln einfach lernen, Rechnen mit Brüchen
Sie lernen hier die wichtigsten Bruchrechnung Regeln und finden somit einen einfachen Einstieg in das Thema Rechnen mit Brüchen. Sie erfahren weiterhin, warum man mit Brüchen rechnen sowie zum Kürzen und Erweitern der Brüche. Insbesondere lernen Sie die Regeln für die Addition, Subtraktion, Division sowie die Multiplikation von Brüchen.
Rechnen mit Brüchen, die Regeln der Bruchrechnung
Mit Brüchen rechnen gilt manchen als mühsam und schwierig, aber das muss nicht sein. Mit einer sorgfältigen Erklärung und etwas Mitdenken lassen sich die Regeln der Bruchrechnung durchaus meistern. Die Probleme stammen oft daher, dass man die Grundlagen nicht sorgfältig genug behandelt. Es gibt wohl keine für alle passende optimale Erklärung und deshalb ist es sinnvoll, auch andere Quellen oder auch Videos zu Rate zu ziehen.
Warum wird überhaupt mit Brüchen gerechnet?
Ganze Zahlen stellen das Ergebnis einer Zählung dar, die angibt, wie viele Einheiten eines Objekts vorhanden sind. In vielen Bereichen möchte man aber Teile einer Einheit betrachten. Etwas braucht vielleicht eine halbe Stunde Zeit und nicht eine ganze, man schneidet eine Tomate in Viertel oder eine Torte in zwölf Stücke. Brüche sind Zahlen, die solche Situationen beschreiben können.
Regeln der Bruchrechnung und die Schreibweise von Brüchen
In der Bruchrechnung bestehen Brüche aus zwei ganzen Zahlen, die durch einen Strich getrennt sind, so sind die Regeln. Die Zahl vor oder über dem Strich ist der Zähler, die andere der Nenner. In dieser Notation ist also 1/2 die Bruchzahl für eine Hälfte und 1/4 die Schreibweise für ein Viertel. Auch wenn es sich um zwei ganze Zahlen handelt, bedeuten sie also je nach Position vor oder nach dem Strich etwas grundsätzlich Verschiedenes. Nach dem Strich steht die Bezeichnung für das Objekt, um das es geht und sinnigerweise ist diese Zahl also der Nenner.
Vor dem Strich gibt die Zahl an, wie viele dieser Objekte gemeint sind. Dieser Idee folgend ist das also der Zähler. Als Beispiel betrachten wir den Bruch 1/5. Das Objekt ist ein Fünftel und das bedeutet, dass dafür eine Einheit in fünf gleiche Teile geteilt wird. Vor dem Strich steht eine 1, also geht es nur um ein Fünftel vom Objekt. Im gleichen Sinn bezeichnet 2/5, 3/5 und 4/5 eben zwei, drei oder vier Teile vom Objekt.
Der Ausdruck 5/5 ist zulässig, wird aber selten verwendet. Er bezeichnet die Aufteilung einer Einheit in fünf gleiche Teile, von denen dann wieder fünf zusammengefasst werden. Daraus entsteht also wieder eine Einheit, die einfach mit 1 bezeichnet wird.
Regeln für das Kürzen und Erweitern von Brüchen in der Bruchrechnung
Die Regel lautet, dass sich ein Bruch nicht ändert, wenn man sowohl den Zähler als auch den Nenner mit derselben ganzen Zahl multipliziert oder durch sie dividiert. Dividieren ist nur möglich, wenn der Zähler und Nenner durch die gleiche ganze Zahl teilbar sind. Ein solches Beispiel haben wir mit 5/5 schon gesehen.
Das Multiplizieren beider Zahlen vor und nach dem Bruchstrich nennt man Erweitern, das Dividieren wird als Kürzen bezeichnet. Leider beschränken sich viele darauf, diese Bruchrechnung Regeln einfach auswendig zu lernen. Besser ist es, sich den Sinn dahinter zu überlegen. Dann wird die Regel nämlich auch viel einfacher im Gedächtnis behalten.
Was passiert, wenn man nur den Nenner mit einer ganzen Zahl multipliziert? Aus 1/2 wird also beispielsweise 1/6. Eine Einheit wird also statt in zwei in dreimal so viele Teile zerlegt. Multiplizieren des Zählers hingegen bedeutet, man nimmt ein Vielfaches der durch den Nenner bezeichneten Teile. In unserem Beispiel ist das 3/6, was dasselbe ist wie 1/2. Das ist unmittelbar klar und wird rein rechnerisch durch Kürzen ermittelt.
Bruchrechnung Regeln für das Addieren und Subtrahieren von Brüchen
Für das Brüche Addieren findet sich auch diese ausführlichere und mit mehr Beispielen versehene Darstellung. Kurz gesagt besteht der erste Schritt darin, durch Erweitern beide Brüche auf denselben Nenner zu bringen. Das erfordert ein gemeinsames Vielfaches beider Nenner. Eine einfache und sicher funktionierende Methode ist es, den einen Nenner mit dem anderen zu multiplizieren. Es kann sein, dass sich die so gefundenen Brüche noch kürzen lassen, aber das ist nicht notwendig.
Wie zählt man zwei Brüche mit demselben Nenner dann zusammen? Man hat dasselbe Objekt, bezeichnet durch den Nenner, und eben zwei Zähler. Man zählt einfach diese zusammen und belässt den Nenner unverändert. Der so ermittelte Bruch kann sich unter Umständen kürzen lassen. Das gleiche gilt auch für die Bruchrechnung Regeln für die Subtraktion.
Weitere Informationen und Details zu den Bruchrechnung Regeln
- Die Bruchrechnung Regeln für die Addition mit Brüchen
- Die Regeln für die Subtraktion mit Brüchen
Bruchrechnung Regeln für das Multiplizieren und Dividieren von Brüchen
Beim Multiplizieren werden beide Zähler und beide Nenner multipliziert, was den Zähler und den Nenner des Produkts ergibt. Für die Begründung und die Regeln der Bruchrechnung betrachten wir wiederum ein Beispiel. Eine Multiplikation eines Bruchs mit 3/1 ist einfach eine Multiplikation mit 3. Statt der vom Zähler des Bruchs angegebenen Anzahl von Objekten nimmt man dreimal soviel. Der Zähler wird also mit 3 multipliziert, der Nenner mit 1 und bleibt deshalb gleich.
Die Multiplikation mit 1/3 bedeutet, man möchte ein Drittel des gegebenen Bruchs ermitteln. Statt der im Nenner angegebenen Zahl teilt man eine Einheit also in dreimal so viele Teile und das bedeutet Multiplikation des Nenners mit 3 und der Zähler bleibt gleich. Jede Multiplikation mit einem Bruch lässt sich in zwei solche Schritte zerlegen. Die Multiplikation mit Brüchen lernen Sie hier.
Für die Division muss man sich nur überlegen, dass eine Division durch eine ganze Zahl wie 3 dasselbe ist wie eine Multiplikation mit 1/3. Eine Division durch 1/3 ist dasselbe wie eine Multiplikation mit 3. Beim Dividieren durch einen Bruch vertauscht man also seinen Zähler und Nenner und multipliziert dann. Wie das genau geht erfahren Sie unter der Bruchrechnung mit der Division.