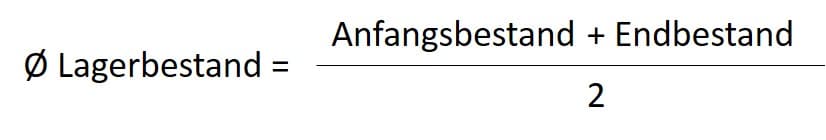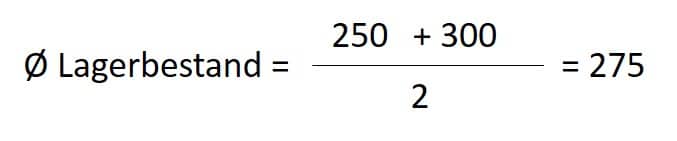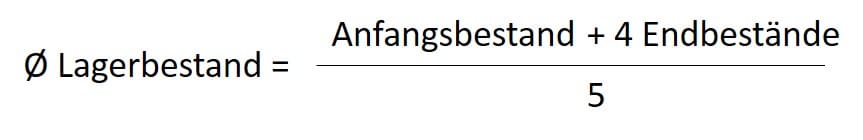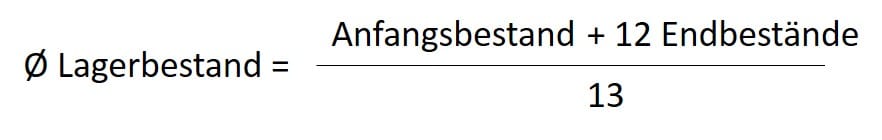Sie lernen mehr zum Thema durchschnittlicher Lagerbestand berechnen. Diese Lagerkennzahl gibt die durchschnittliche Stückzahl einer Periode wieder. Hier lernen Sie weiterhin das Berechnen des Lagerbestands sowie der Kapitalbindung mit Beispiel und Formel. Ebenfalls erhalten Sie am Ende des Beitrags Übungen bzw. Aufgaben, um Ihr Wissen zu festigen bzw. zu vertiefen.
Wie berechnet man den durchschnittlichen Lagerbestand?
Bei der Berechnung des durchschnittlichen Lagerbestands benötigt man zumindest den Anfangsbestand und den Endbestand als Stückzahl.
Die Formel für den durchschnittlichen Lagerbestand
Mit dieser einfachen Formel kann man die durchschnittlichen Lagerbestände berechnen. Sie brauchen dazu mindestens den Anfangsbestand und den Endbestand der Ware oder des Materials. Der Teiler ergibt sich aus der Addition des Anfangsbestand und der Endbestände. In diesem Fall der Anfangsbestand und ein Endbestand = 2.
Durchschnittlicher Lagerbestand am Beispiel besser verstehen
Beispiel: Im Lager beträgt der Anfangsbestand zum 01.01. 250 Stück, der Endbestand zum 31.12. beträgt 300 Stück.
Somit ergibt sich ein durchschnittlicher Lagerbestand von 275 Stück.
Weitere Formeln für das Quartal und für den Monat beim Lagerbestand berechnen
Genauer ist die Kennzahl, wenn mehrere Endbestände zu addieren sind. Folgende Formeln sind noch sinnvoll. Der durchschnittliche Lagerbestand auf Quartalsbasis sowie der Monatsbasis. Die Formeln lauten dann:
Die Formel auf Quartalsbasis
Formel: (AB + 4 EB) / 5
Die Formel auf Monatsbasis
Formel: (AB + 12 EB) / 13
Je mehr Werte angesetzt sind, je genauer ist der durchschnittliche Lagerbestand zu berechnen. Je höher ist also die Genauigkeit der Kennzahl.
Die durchschnittliche Kapitalbindung berechnen
Eine durchschnittliche Kapitalbindung entspricht dem durchschnittlichen Lagerbestand in Stück, jedoch in Geld zum Beispiel Euro bewertet. Die durchschnittliche Kapitalbindung ist also das Produkt aus Stückzahl und Einstandspreis der Ware bzw. des Materials.
Das Beispiel für die Kapitalbindung
Beispiel: Der durchschnittliche Lagerbestand beträgt 275 Stück. Der Einstandspreis der Ware beträgt 17 € pro Stück.
Die Berechnung der Kapitalbindung
Berechnung: Durchschnittliche Kapitalbindung = durchschnittlicher Lagerbestand x Einstandspreis
- Durchschnittliche Kapitalbindung = 275 Stück x 17 € = 4675 €
Somit ergibt sich die Aussage, das die durchschnittliche Kapitalbindung 4675 € im Jahr beträgt.
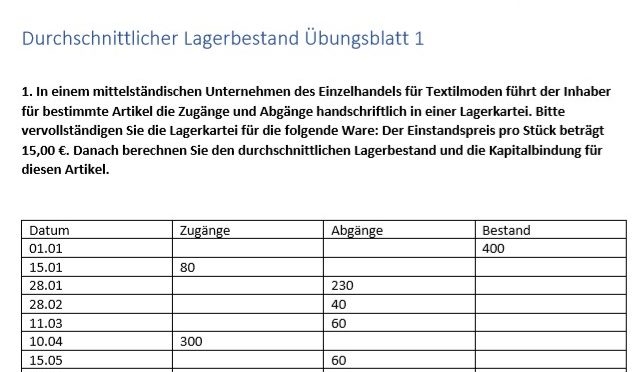
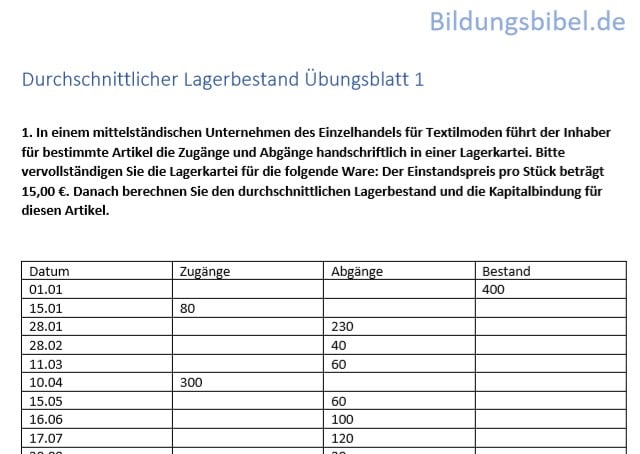
Durchschnittlicher Lagerbestand Übungen und Aufgaben, kostenlos downloaden
Sie finden hier spezielle Übungen bzw. Aufgaben für den Lagerbestand zu berechnen. Die Arbeitsblätter dürfen Sie kostenlos downloaden sowie zum Üben benutzen.
Weitere Infos zum Thema durchschnittlicher Lagerbestand
Diese Beiträge zum Thema könnten Sie ebenfalls interessieren:
- Den Wareneinsatz berechnen mit Formel oder Schema, Kalkulation, Beispiel und Übungen.
- Die Lagerumschlagshäufigkeit berechnen, Umschlag, Formel und Beispiel.
- Die durchschnittliche Lagerdauer berechnen mit Formel sowie Beispiel.
- Die Lagerbestände mit der Andler-Formel berechnen.