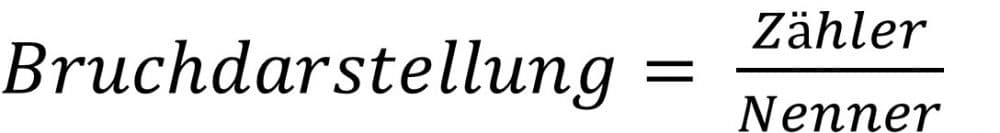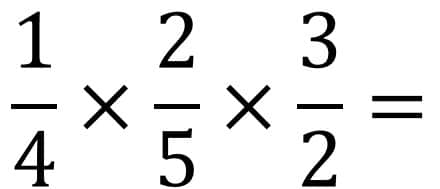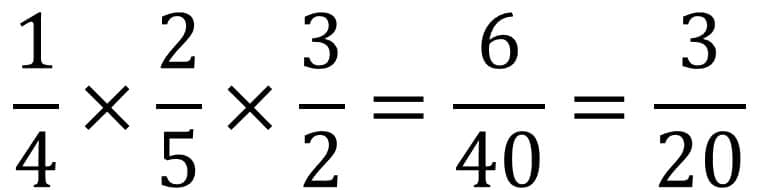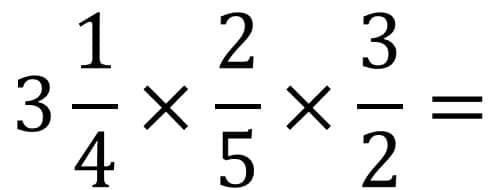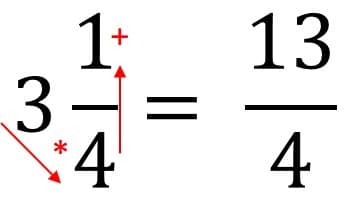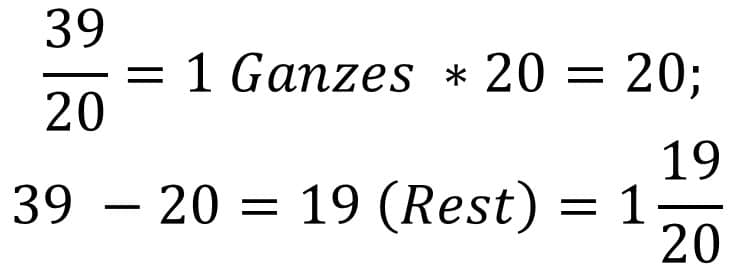Hier lernen Sie in einfacher Form die Bruchrechnung mit Mal oder der Multiplikation. Sie lernen am Beispiel, wie das Malnehmen von Brüchen funktioniert und erhalten eine Anleitung. Weiterhin erhalten Sie Übungen und Aufgaben zum Thema am Ende vom Beitrag.
Inhaltsverzeichnis
Bruchrechnung Multiplikation Begriff und Definition zum Multiplizieren mit Brüchen
Bei der Multiplikation spricht man auch von Multiplikator, also die Zahl die mal genommen oder multipliziert wird. Weiterhin von Multiplikand, die Zahl mit der man mal nimmt bzw. multipliziert. Unter Produkt versteht man das Ergebnis der Multiplikation. Das Wort Multiplikation kommt aus dem lateinischen und bedeutet soviel wie Vervielfachung. Weiterhin sind im Sprachgebrauch „Mal-nehmen“ oder „Mal-Rechnen“.
Regeln zur Bruchrechnung mit der Multiplikation oder Mal
Der obere Wert eines Bruchs nennt sich Zähler, der Wert unter dem Bruch nennt sich Nenner. Hier lernen Sie die Grundregeln der Multiplikation von Brüchen, an welche Sie sich halten sollten bzw. müssen.
Bei der Multiplikation von Brüchen, müssen Sie die Brüche nicht gleichnamig machen. Sie multiplizieren den Zähler mit dem Zähler und den Nenner mit dem Nenner. Sie können jeden Zähler mit jedem Nenner kürzen, um die Multiplikation zu vereinfachen. Sollten Sie mit Ganzzahlen multiplizieren bzw. Mal-Rechnen, so müssen Sie die Ganzzahlen in einen unechten Bruch umwandeln. Danach können Sie mit der Multiplikation beginnen.
Anleitung mit Beispiel für die Bruchrechnung mit der Multiplikation
Hier erhalten Sie eine Anleitung mit einem einfachen Beispiel. Beim Bruchrechnen mit der Multiplikation oder Mal-nehmen gehen Sie folgendermaßen vor:
Aufgabe für das Multiplizieren richtig aufschreiben
Schritt 1: Sie schreiben die Brüche nebeneinander und versehen die Brüche mit dem Operator Mal (x). In diesem einfachen Beispiel geht es um die Grundregeln der Bruchrechnung mit der Multiplikation bzw. Mal.
Multiplizieren von Zähler und Nenner beim Bruchrechnen
Der obere Wert eines Bruchs, nennt man Zähler und den unteren Wert eines Bruchs nennt man Nenner. Bei der Multiplikation müssen wir die Brüche nicht gleichnamig oder gleichwertig machen.
In diesem Beispiel werden die Zähler mit den Zählern und die Nenner mit den Nennern multipliziert. Das Ergebnis am Ende ist nochmals zu kürzen. Im Nachfolgenden entstehen folgende Einzelschritte.
- 1 * 2 * 3 = 6 (Zähler)
- 4 * 5* 2 = 40 (Nenner)
Der Bruch lässt sich durch 2 kürzen, somit erhalten wir 6/2 = 3 und 40/2 = 20
Multiplikation mit Ganzzahlen und die Umwandlung in unechte Brüche
Hier lernen Sie, wie Sie mit Ganzzahlen umgehen und diese in unechte Brüche umwandeln.
In obigem Bruch sehen wir die Ganzzahl 3, welche wir bei der Multiplikation bzw. dem Mal-nehmen mit in den Bruch ziehen müssen. Dadurch verwandelt sich der gemischte Bruch in einen unechten Bruch. So gehen Sie vor, um den unechten Bruch zu erzeugen. Die Ganzzahl * Nenner + Zähler = unechter Bruch. Der Nenner bleibt gleich 3 * 4 + 1 = 13 (Zähler), 4 (Nenner)
Multiplizieren mit Ganzzahl nach der Umwandlung in einen unechten Bruch
Nach dem Umwandeln in einen unechten Bruch wird das Beispiel wieder ganz normal multipliziert, wie in der ersten Aufgabe. Die einzelnen Teilschritte sind nochmals folgende:
- 13 * 2 * 3 = 78 (Zähler)
- 4 * 5* 2 = 40 (Nenner)
Der Bruch lässt sich durch 2 kürzen, somit erhalten wir 78/2 = 39 und 40/2 = 20
Umrechnung unechter Bruch in einen gemischten Bruch
In dieser Beispielsaufgabe müssen wir nun einen unechten Bruch in einen gemischten Bruch überführen. Dazu gehen Sie folgendermaßen vor: Beispielsaufgabe: (39 / 20). Indem Sie jetzt die 39 durch die 20 teilen, erhalten Sie eine Zahl größer als 1.
Danach rechnen Sie Nenner mal die Zahl vor dem Komma. In unserem Fall die Zahl 1 * 20 = 20. Dann gehen Sie hin und ziehen vom Zähler die errechnete Zahl ab. Sie erhalten den Rest = 39 – 20 = 19 (Rest). So können Sie jeden beliebigen unechten Bruch in eine gemischte Form überführen.
Bruchrechnung Aufgaben, Übungen oder Arbeitsblätter für die Multiplikation PDF
Hier können Sie Ihr Wissen nochmals überprüfen. Diese Bruchrechnung Aufgaben, Übungen oder Arbeitsblätter sind speziell für das Rechnen mit Mal oder Multiplikation angefertigt.
Sie können die Aufgaben als PDF-Datei herunterladen und ausdrucken. Lösungen können Sie mit diesem Rechner für Brüche nachvollziehen.
Weitere Infos
Diese Infos könnten Sie ebenfalls interessieren: