Weiterbildung – Online lernen – Kaufmännisches Rechnen – Einfacher & zusammengesetzter Dreisatz lernen, Beispiele & Übungen kostenlos
Der Dreisatz ist ein bewährtes mathematisches Verfahren, um proportionale Zusammenhänge zu verstehen und zu berechnen. Ob im Alltag, in der Schule oder im Berufsleben – der Dreisatz ist ein Werkzeug, das nahezu überall Anwendung findet.
Er lässt sich in zwei Arten unterteilen: den einfachen Dreisatz für direkte Verhältnisse und den Dreisatz für indirekte Verhältnisse. Bei einem direkten Verhältnis führt eine Zunahme der einen Größe auch zur Zunahme der anderen. Beim indirekten Verhältnis führt eine Zunahme der einen Größe zur Abnahme der anderen.
Mithilfe von beispielhaften Aufgaben und interaktiven Übungen kann man die Anwendung des Dreisatzes erlernen und üben. Die Arbeitsblätter zum Download ermöglichen eine gezielte Vertiefung. Beim zusammengesetzten Dreisatz, der mehr als zwei proportionale Größen enthält, helfen schrittweise Anleitungen dabei, komplexe Probleme zu lösen.
Einfacher Dreisatz
Der einfache Dreisatz hat seinen Namen bekommen, da er aus drei Sätzen besteht, wenn es um die Lösung geht. Diese werden weiter unten näher erklärt. Das direkte Verhältnis wird in der Mathematik auch proportionales oder gerades Verhältnis genannt. Das indirekte Verhältnis wird bezeichnet als anti-proportionales oder ungerades Verhältnis.
Drei Sätze sind entscheidend
Der erste Satz beim Dreisatz lernen, ist der Bedingungssatz. Der zweite Satz ist der Fragesatz. Der dritte Satz ist der Bruchsatz, also die eigentliche Vorgehensweise der Berechnung auf dem Bruchstrich.
Anleitung zum Dreisatz
Sie erhalten hier eine Anleitung oder Vorgehensweise sowie Übungen und Aufgaben, um den Dreisatz zu lernen. Da die Aufgaben meist als Textaufgaben gestellt werden, ist es als erstes wichtig, den Text richtig zu lesen. Danach geht es zum Verstehen der Aufgabenstellung. In der Folge wird aus diesem Text der Fragesatz und der Bedingungssatz aufgebaut.
Aus dem Bedingungssatz und Fragesatz kann man dann den Bruchsatz bilden. Hierbei spielt das logische Denken eine wichtige Rolle. Sie finden auch eine detaillierte Vorgehensweise und eine Lösung anhand einem Beispiel erklärt, wie Sie auf den Bruchsatz kommen.
Indirektes oder ungerades Verhältnis
Sie finden hier das Beispiel mit dem indirekten Verhältnis oder ungeraden Verhältnis beim Dreisatz berechnen. Man sagt manchmal auch anti-proportionales Verhältnis dazu, dass hängt meist von der Schulform ab, die Sie gerade besuchen.
Beispiel für das indirekte Verhältnis
5 Arbeiter eines Reinigungsteams benötigen zum Reinigen von Räumen 270 Minuten. Welche Arbeitszeit muss veranschlagt werden, wenn aus Krankheitsgründen 2 Arbeiter des Reinigungsteams nicht arbeiten können?
Aufbau vom Bedingungssatz
In diesem Beispiel gibt es 5 Arbeiter, die Räume reinigen und 270 Minuten benötigen, damit haben wir den
- Bedingungssatz: 5 Arbeiter = 270 Minuten
Aufbau vom Fragesatz
Die zweite Angabe in diesem Beispiel bildet den Fragesatz: 2 Arbeiter werden krank, wie lange brauchen die Arbeiter?
- Fragesatz: 3 Arbeiter = x Minuten
Jetzt kommen wir zum Bruchsatz
Jetzt kommt die schwerste Entscheidung! Wie soll das auf den Bruchstrich? Jetzt ist Logik gefragt, um zu entscheiden ob hier ein direktes Verhältnis oder ein indirektes Verhältnis vorliegt.
- Ein direktes Verhältnis prüfen Sie mit der Gedankenstütze: Je weniger, desto weniger und Je mehr, desto mehr.
- Ein indirektes Verhältnis prüfen Sie mit der Stütze: Je mehr, desto weniger oder je weniger desto mehr.
In unserem Beispiel liegt ein indirektes Verhältnis vor. Da 5 Arbeiter 270 Minuten benötigen und es jetzt nur noch 3 Arbeiter sind, die die gleiche Tätigkeit ausführen. Das heißt je weniger Arbeiter desto mehr Zeit wird benötigt. Jetzt auf zum Bruchsatz:
- 5 Arbeiter = 270 Minuten
- 3 Arbeiter = x Minuten
- x = 270 x 5 / 3 = 450 Minuten
In der Bruchdarstellung oder Formel sieht das so aus:

Sie sehen, das die Angabe, welche über x steht als erstes auf den Bruchstrich geschrieben wird. Danach rechnen Sie 5 durch 3. Diese Angabe wird einfach aus der Aufstellung von Bedingungssatz und Fragesatz übertragen. Das, was oben steht bleibt beim indirekten Verhältnis über dem Bruchstrich sowie das was unten steht, kommt unter den Bruchstrich. Dann nur noch berechnen und den Antwortsatz aufschreiben.
- Die Antwort: Mit 3 Arbeitern, werden für die gleiche Tätigkeit 450 Minuten benötigt.
Direktes oder gerades Verhältnis
Das Beispiel mit direktem Verhältnis man sagt auch proportionales oder gerades Verhältnis beim Dreisatz lernen.
Beispiel beim direkten Verhältnis
Ein Artikel kostet 18,00 €. Wie viel kosten 20 Stück dieses Artikels?
Aufbau vom Bedingungssatz
In diesem Beispiel gibt es einen Artikel mit dem Preis von 18,00 €, damit haben wir schon den Bedingungssatz:
- 1 Artikel = 18,00 €
Aufbau vom Fragesatz
Die zweite Angabe in diesem Beispiel bildet den Fragesatz: Wie viel kosten 20 Stück?
- 20 Artikel = x €
Jetzt kommen wir wieder zum Bruchsatz
Die Regeln sind die gleichen wie oben. Wenn Sie das schon verstanden haben, so können Sie diesen Teil überspringen und gleich zur Berechnung übergehen. Jetzt kommt die schwerste Entscheidung! Wie soll das auf den Bruchstrich? Jetzt ist wieder die Logik gefragt, um zu entscheiden ob hier ein direktes Verhältnis oder ein indirektes Verhältnis vorliegt.
- Ein direktes Verhältnis prüfen Sie mit der Gedankenstütze: Je weniger, desto weniger und Je mehr, desto mehr.
- Ein indirektes Verhältnis prüfen Sie mit der Stütze: Je mehr, desto weniger oder je weniger desto mehr.
In unserem Beispiel für das Dreisatz lernen liegt jetzt ein direktes Verhältnis vor, da 1 Artikel 18,00 € kostet und jetzt werden 20 Stück gekauft. Das heißt je mehr Artikel, desto mehr Kosten werden verursacht. Jetzt auf zum Bruchsatz:
- 1 Artikel = 18,00 €
- 20 Artikel = x €
- x = 18,00 x 20 / 1 = 360,00 €
In der Bruchdarstellung bzw. Formel sieht das so aus
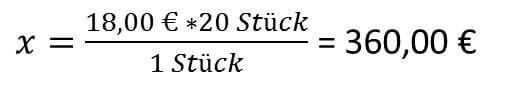
Sie sehen, das die Angabe, welche über x steht als erstes auf den Bruchstrich geschrieben wird, das ist generell so. Danach folgt 20 durch 1. Diese Angabe wird einfach umgekehrt aus der Aufstellung vom Bedingungssatz und Fragesatz übertragen. Das was oben steht, steht beim direkten Verhältnis unter dem Bruchstrich und das was unten steht, kommt auf den Bruchstrich. Jetzt noch ausrechnen und den Antwortsatz schreiben.
- Die Antwort: Für 20 Artikel müssen 360,00 € aufgebracht werden.
Zusammengesetzter Dreisatz lernen
Beim zusammengesetzten Dreisatz, gibt es mehrere Angaben, die Sie zu berücksichtigen haben. Selbst wenn Sie verstanden haben, wie sie mit dem indirekten oder direkten Verhältnis umgehen, scheiden sich an diesem Punkt wieder einmal die Geister.
Dabei ist der zusammengesetzte Dreisatz nichts anderes als mehrere kleine indirekte oder direkte Verhältnisse und die Vorgehensweise ist fast ähnlich. Hier lernen Sie den Umgang an einem Beispiel.
Anleitung und Beispiel
Beispiel: In einer Fabrik erzeugen 7 Maschinen in 14 Tagen 19600 Ersatzteile, wenn 8 Stunden täglich gearbeitet wird. Aufgrund eines Großauftrages sollen 30000 Ersatzteile produziert werden. Jedoch müssen die Maschinenzeiten auf 6 Stunden pro Tag gekürzt werden, da noch andere Aufträge gearbeitet werden. Dafür wird 1 Maschine mehr eingesetzt. Wie viele Tage werden benötigt, um den Auftrag abzuarbeiten?
Bedingungssatz aufbauen
In diesem Beispiel gibt es 7 Maschinen. Diese benötigen 14 Tagen bei einer täglichen Arbeitszeit von 8 Stunden. Sie erzeugen insgesamt 19600 Ersatzteile. Nun können wir damit den Bedingungssatz aufbauen:
- 7 Maschinen = 8 Stunden = 19600 Ersatzteile = 14 Tage
Fragesatz aufbauen
Die zweite Angabe in diesem Beispiel bildet den Fragesatz: Wie viele Tage werden benötigt, um einen Auftrag von 30000 Ersatzteilen, in 6 Stunden täglich mit einer Maschine mehr fertig zustellen?
- 8 Maschinen = 6 Stunden = 30000 Ersatzteile = x Tage
Bruchstrich, Bruchsatz oder Formel aufbauen
Wie soll das jetzt auf den Bruchstrich? Ganz einfach! Sie prüfen jedes Verhältnis gegen x Tage und beachten die Regeln für ein direktes oder indirektes Verhältnis.
Hier nochmals zur Erinnerung:
- Ein direktes Verhältnis prüfen Sie mit der Gedankenstütze: Je weniger, desto weniger und Je mehr, desto mehr.
- Ein indirektes Verhältnis prüfen Sie mit der Stütze: Je mehr, desto weniger oder je weniger desto mehr.
In unserem Beispiel liegen jetzt eventuell unterschiedliche Verhältnisse vor. Deswegen prüfen wir Verhältnis für Verhältnis durch und halten uns an die Regeln, was den Bruchstrich angeht. Jetzt auf zum Bruchsatz:
- 7 Maschinen = 8 Stunden = 19600 Ersatzteile = 14 Tage
- 8 Maschinen = 6 Stunden = 30000 Ersatzteile = x Tage
Verhältnis 1 prüfen
- 7 Maschinen = 14 Tage
- 8 Maschinen = x Tage
Lösung: Das was über x steht werden wir auf den Bruchstrich schreiben. Jedoch nur einmal, ganz am Anfang. Jetzt prüfen wir 7 Maschinen brauchen 14 Tage. Wenn wir 8 Maschinen haben, brauchen wir weniger Tage. Somit liegt ein indirektes oder ungerades Verhältnis vor. Nun übernehmen wir 7 durch 8, wobei die 7 oben steht und die 8 unter dem Bruchstrich. In der Bruchdarstellung sieht das so aus
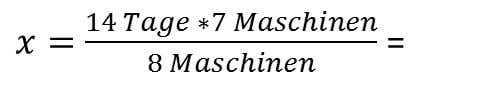
Verhältnis 2 prüfen
- 8 Stunden = 14 Tage
- 6 Stunden = x Tage
Lösung: Jetzt prüfen wir 8 Stunden tägliche Arbeitszeit dafür brauchen wir 14 Tage. Wenn wir 6 Stunden pro Tag arbeiten, brauchen wir mehr Tage. Somit liegt ein indirektes oder ungerades Verhältnis vor. Nun übernehmen wir 8 durch 6, wobei die 8 oben steht und die 6 unter dem Bruchstrich. In der Bruchdarstellung sieht das so aus:
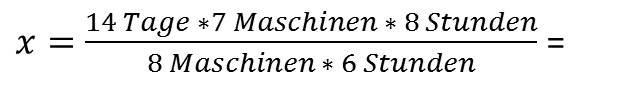
Verhältnis 3 prüfen
- 19600 Ersatzteile = 14 Tage
- 30000 Ersatzteile = x Tage
Lösung: Jetzt prüfen wir, in 14 Tagen kann ich 19600 Ersatzteile herstellen. Wenn ich mehr Ersatzteile herstellen will, brauche ich mehr an Tagen. Somit liegt ein direktes oder gerades Verhältnis vor. Nun übernehmen wir 30000 durch 19600, wobei die 30000 oben steht und die 19600 unter dem Bruchstrich. In der Bruchdarstellung mit Formel sieht das so aus:
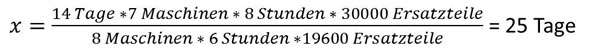
Antwortsatz schreiben
Antwort: Für die Produktion von 30000 Ersatzteilen, werden bei einer täglichen Arbeitszeit von 6 Stunden und dem Einsatz von 8 Maschinen 25 Tage benötigt.
Dreisatz Übungen, Aufgaben & Arbeitsblätter kostenlos
Die Dreisatz Übungen, Aufgaben oder Arbeitsblätter zum direkten und indirekten Verhältnis sowie zum zusammengesetzten Dreisatz lernen, können Sie hier kostenlos herunterladen. Die Übungsblätter bestehen jeweils aus 10 Aufgaben, um den Dreisatz zu lernen.
Video
In diesem Video von Lehrer Schmidt können Sie den Dreisatz nochmals in Ruhe nachvollziehen.
Weiterführende Informationen
Diese Informationen könnten Sie ebenfalls interessieren:
- Die Webseite Mathepower bietet eine einfache und benutzerfreundliche Möglichkeit, den Dreisatz zu berechnen. Der Dreisatz ist eine mathematische Methode, um Proportionen und Verhältnisse zu lösen. Auf der Seite können Benutzer ihre Ausgangswerte eingeben und erhalten dann das Ergebnis des Dreisatzes. Die Seite bietet eine klare Erklärung sowie Beispiele zur Anwendung des Dreisatzes. Sie eignet sich sowohl für Schüler als auch für Erwachsene, die ihr mathematisches Verständnis verbessern möchten.




